Question

You are throwing a ball straight up and then catching it as it returns to your hand. When the ball leaves your hand, its momentum is in the upward direction but when it returns to your hand, its momentum is in the downward direction. During its flight above your hand, what happens to the ball's initial upward momentum?(A) The upward momentum is converted into gravitational potential energy. (B) The upward momentum is converted into kinetic energy. (C) The upward momentum is converted into thermal energy. (D) The upward momentum is transferred to the earth.

Answer 1

(D) The upward momentum is transferred to the earth.

Step-by-step explanation:

We can consider the ball + the Earth as a single, isolated system: therefore, the total momentum of the two objects must be conserved.

Assuming the Earth is initially at rest (so, its initial momentum is zero:
`p_(iE)=0`, and calling
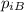`p_(iB)` the initial momentum of the ball, the total initial momentum of the ball+Earth system is

`p_i = p_(iB) + p_(iE)= p_(iB)`

When the ball returns to your hand, its momentum has changed direction, so the final momentum of the ball is

`p_(fB) = -p_(iB)`

And since the total momentum of the ball+Earth system must be conserved:

`p_f = p_(fB)+p_(fE) = p_i`

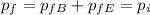
We can write:

`p_(fB)+p_(fE) = p_(iB)\\-p_(iB) + p_(fE) = p_(iB)\\p_(fE) = 2p_(iB)`

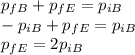
Which means that the variation of momentum of the ball has converted into variation of momentum of the Earth. Of course, given the huge mass of the Earth, it is not possible to observe this variation of momentum of the Earth (because the corresponding variation of velocity is negligible).