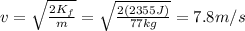Question

A student, starting from rest, slides down a water slide. On the way down, a kinetic frictional force (a nonconservative force) acts on her. The student has a mass of 77 kg, and the height of the water slide is 12.0 m. If the kinetic frictional force does -6.7 × 103 J of work, how fast is the student going at the bottom of the slide?

Answer 1

7.8 m/s

Step-by-step explanation:

At the top of the slide, the mechanical energy of the student is just gravitational potential energy, given by:

`E_i = U_i =mgh`

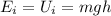
where m=77 kg is the mass of the student, g=9.8 m/s^2 is the gravitational acceleration, h=12.0 m is the height of the slide. Substituting,

`E_i=(77 kg)(9.8 m/s^2)(12.0 m)=9055 J`

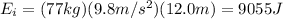
While she slides down, the frictional force does

`W=-6.7\cdot 10^3 J=-6700 J`

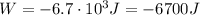
on her. So, the final mechanical energy of the student at the bottom of the slide is

`E_f = E_i+W=9055 J-6700 J=2355 J`

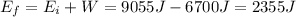
And this energy is just equal to the final kinetic energy of the student, since its potential energy is just zero (at the bottom of the slide, h=0):

`E_f = K_f = (1)/(2)mv^2`

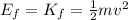
where v is the final speed of the student. Solving for v,

`v=\sqrt{(2K_f)/(m)}=\sqrt{(2(2355 J))/(77 kg)}=7.8 m/s`