Question

What is the equation of the midline for the function y=3cos (x-pi)-4

Answer 1

3 cos((x - π ) - 4 = 3 cos(x) - 4 since cos(x-π) = cos(x)

-1 ≤ cos(x) ≤ 1

-3 ≤ 3cos(x) ≤ 3

-3-4 ≤ 3 cos(x)-4 ≤ 3-4

-7 ≤ 3 cos(x) ≤ -1

The range is -7 to -1 so the midpoint is (-7-1)/2 = -4

y = -4 is the equation of the midline

Explanation:

there you go

Answer 2

Answer with explanation:

y=3 Cos (x-π)-4

The Equation of mid line of a function can be obtained by finding the Mean of Maximum and Minimum Value of the function and then finding the equation of line passing through that point.

→Cos (x-π)=Cos[-(π-x)]= -Cos x, Cos (-x)=Cos x,and,Cos(π-x)= -Cos x,as Cos x is Negative in Second Quadrant.

The above function can be written as

y= -3 Cos x -4

→ -1 ≤ Cos x ≤ 1

→ -3≤-3 Cos x≤3

→ -3 -4≤ -3 Cos x -4≤3-4

→ -7 ≤ -3 Cos x -4 ≤ -1

The Maximum Value of the function , 3 Cos (x-pi)-4, is -1, and Minimum value of the function is ,-7.

Mean of Maximum and Minimum is

`=(-1+-7)/(2)=(-8)/(2)= -4`

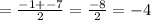
→Equation of mid line of the function, y=3 Cos (x-pi)-4, is

y = -4