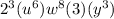Question

Find the least common multiple of these two expressions. 24y^3u^6w^8 and 2u^6w^5

Answer 1

`24(u ^ 6)w ^ 8(y ^ 3)`

Explanation:

To find the common minimum multiple between two expressions, you must choose the common factors with their greatest exponent and the non-common factors with their greatest exponent.

For this problem we have the following expressions:

`24y ^ 3u ^ 6w ^ 8`

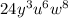
and

`2u^6w^5`

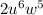
To begin with, you can decompose the term 24 into its prime factors.

24 | 2

12 | 2

6 | 2

3 | 3

one

`24 =(2 ^ 3)3`

Then the previous expressions are as follows.

`2 ^ 33y ^ 3u ^ 6w ^ 8`

and

`2u ^ 6w ^ 5`

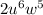
We take the common terms first with their greatest exponent:

`2 ^ 3(u ^ 6)w ^ 8`

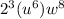
Now the terms are not common with its greatest exponent

`3(y ^ 3)`

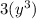
Finally the multiple common multiple is:

`2 ^ 3(u ^ 6)w ^ 8(3)(y ^ 3)`

`24(u ^ 6)w ^ 8(y ^ 3)`