Question

Help please!!!!!!!!!!!!!

Answer 1

position 1 5 8 12 19 25

term -8 8 20 36 64 88

Explanation:

(n - 1) is position ( n ∈ N)

d is the distance between the numbers in the sequence

a1 is the first number in the sequence

we have the fuction: a(n) = a1 + (n - 1)d

see in the table, with position = 1, term = -8 => a1 + d = -8

position = 25, term = 88 => a1 + 25d = 88

=> we have: a1 + d = -8

a1 + 25d = 88

=> a1 = -12

d = 4

=> a(n) = -12 + 4(n - 1)

=> term = 8, position = (8 + 12)/4 = 5

position = 8, term = -12 + 4.8 = 20

term = 36, position = (36 + 12)/4 = 12

position = 19, term = -12 + 4.19 = 64

Answer 2

The required table is:

Position 1 5 8 12 19 25

Term -8 8 20 36 64 88

Explanation:

The general formula for arithmetic sequence is:

`a_n=a_1+(n-1)d`

where n is the nth term, a₁ is the first term and d is the difference.

Looking at the table, we know that

a₁ = -8 and

a₂₅ = 88

We can find the common difference d:

`a_n=a_1+(n-1)d\\n=25, a_1=-8, a_(25)=88\\a_(25)=a_1+(25-1)d\\88=-8+24(d)\\88+8=24\:d\\96=24\:d\\d=(96)/(24)\\d=4`

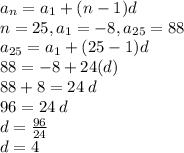
So, we have d = 4

Now we can fill the remaining table.

We have to find position n, when term (a_n) is 8

`a_n=a_1+(n-1)d\\8=-8+(n-1)4\\8=-8+4n-4\\8=-12+4n\\8+12=4n\\20=4n\\n=(20)/(4)\\n=5`

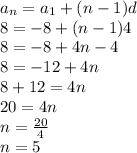
So, when term is 8, position is 5

We have to find term a_n when position n is 8

`a_n=a_1+(n-1)d\\a_8=-8+(8-1)4\\a_8=-8+7(4)\\a_8=-8+28\\a_8=20`

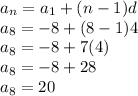
So, when position is 8 term is 20

We have to find position n, when term (a_n) is 36

`a_n=a_1+(n-1)d\\36=-8+(n-1)4\\8=-8+4n-4\\8=-12+4n\\36+12=4n\\48=4n\\n=(48)/(4)\\n=12`

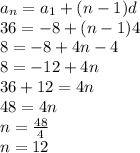
So, when term is 36, position is 12

We have to find term a_n when position n is 19

`a_n=a_1+(n-1)d\\a_(19)=-8+(19-1)4\\a_(19)=-8+18(4)\\a_(19)=-8+72\\a_(19)=64`

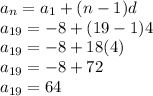
when position is 19 term is 64

So, the required table is:

Position 1 5 8 12 19 25

Term -8 8 20 36 64 88