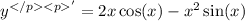Question

Use logarithmic differentiation to find the derivative of the function. y = x2cos x Part 1 of 4 Using properties of logarithms, we can rewrite ln y = ln(x2cos x) as

Answer 1

`{y}^(</p><p>') = 2x \cos(x) - {x}^(2) \sin(x)`

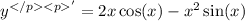
Step-by-step explanation

The given function is

`y = {x}^(2) \cos(x)`

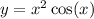
We take natural log of both sides;

`ln(y) = ln({x}^(2) \cos(x) )`

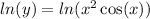
Recall and use the product rule of logarithms.

`ln(AB) = ln(A ) + ln(B)`

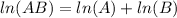
This implies that:

`ln(y) = ln({x}^(2) ) + ln( \cos(x) )`

`ln(y) = 2 ln({x} ) + ln( \cos(x) )`

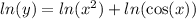
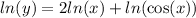
We now differentiate implicitly to obtain;

`\frac{ {y}^(</p><p>') }{y} = (2)/(x) - ( \sin(x) )/( \cos(x) )`

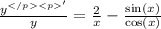
Multiply through by y,

`{y}^(</p><p>') = y( (2)/(x) - ( \sin(x) )/( \cos(x) ) ))`

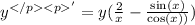
Substitute y=x²cosx to obtain;

`{y}^(</p><p>') = {x}^(2) \cos(x) ( (2)/(x) - ( \sin(x) )/( \cos(x) ) ) )`

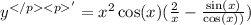
Expand:

`{y}^(</p><p>') = 2x \cos(x) - {x}^(2) \sin(x)`