Answer:
(4, 3)
Explanation:
If a point O(x, y) divides a line segment AB with end points at A(
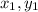 ) and B(
) and B(
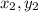 ) in the ratio of n:m, then the location of O is at:
) in the ratio of n:m, then the location of O is at:
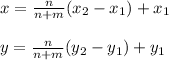
Given that Nates house is located at (-2,4) while the park is located at (10,2). Macs house if it is 1/2 of the distance from Nates house to the park (that is in the ratio of 1:1). Let (x, y) be the coordinate of Macs house, therefore:
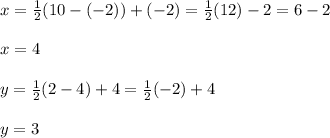
The location of Macs house is (4, 3)