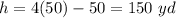Question

PYRAMIDS The Great Pyramid in Giza, Egypt has a square base with side lengths of 5x yards and a height of 4x –

50 yards. The volume of the Great Pyramid is 3,125,000 cubic yards. Use a calculator to find the value of x and the
dimensions of the pyramid.

Answer 1

The value of x is equal to
`50\ yd`

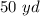
The side length of the base b is
`250\ yd`

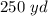
The height h is
`150\ yd`

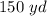
Explanation:

we know that

The volume of a square Pyramid is equal to

`V=(1)/(3) b^(2)h`

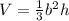
where

b is the length side of the square base

h is height of the pyramid

In this problem we have

`V=3,125,000\ yd^(3)`

`b=5x\ yd`

`h=4x-50\ yd`

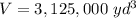
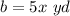
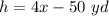
substitute and solve for x

`3,125,000=(1)/(3) (5x)^(2))(4x-50)`

`9,375,000=100x^(3) -1,250x^(2)\\ \\100x^(3) -1,250x^(2)-9,375,000=0`

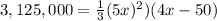
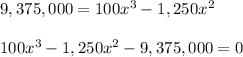
using a calculator

The value of x is equal to

`x=50\ yd`

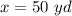
Find the dimensions of the pyramid

The side length of the base b

`b=5(50)=250\ yd`

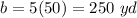
The height h

`h=4(50)-50=150\ yd`