Answer with explanation:
The two Starting Points used by Eowyn for deriving Distance formula:
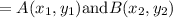
Then Eowyn has Drawn the point C
→ She Draw a Horizontal Line From Point A, and a vertical line from point B, and then the point where these lines intersect was named the point
 .
.
→ She Supposed, AC=b, BC=a
and then, AB=c
→Ruler Postulate

With the Help of Pythagorean Theorem and Substitution Property
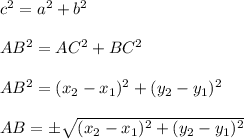
As, Distance can't be negative
So,
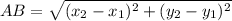
⇒ Here, a and b should be
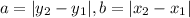
Option C:→→ Eowyn didn't correctly derive the distance formula. She drew in her auxiliary segments correctly, but she didn't define a, b, and c correctly in order to apply them in the Pythagorean Theorem.