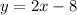Question

Find an equation of the tangent to the curve at the given point by both eliminating the parameter and without eliminating the parameter.x = 6 + ln(t), y = t2 + 3, (6, 4)

Answer 1

`y=2x-8`

Explanation:

The given parametric equation is;

`x=6+ln(t),y=t^2+3`

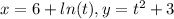
BY ELIMINATING THE PARAMETER

To eliminate the parameter we make
`t` the subject in one equation and put it inside the other.

We make
`t` the subject in
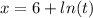`x=6+ln(t)` because it is easier.

`\Rightarrow x-6=ln(t)`

`\Rightarrow {e}^(x-6)=e^(ln(t))`

`\Rightarrow {e}^(x-6)=t`

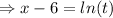
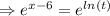
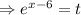
Or

`t={e}^(x-6)`

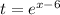
We now substitute this into
`y=t^2+3`.

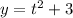This gives us;

`y=(e^(x-6))^2+3`.

`\Rightarrow y=e^(2(x-6))+3`.

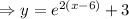We have now eliminated the parameter.

The equation of the tangent at (6,4) is given by;

`y-y_1=m(x-x_1)`

where the gradient function is given by;

`(dy)/(dx)=2e^(2(x-6))`

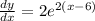
We substitute
`x=6` into the gradient function to obtain the gradient.

`\Rightarrow m=2e^(2(6-6))`

`\Rightarrow m=2e^0`

`\Rightarrow m=2`

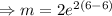
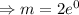
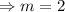
The equation of the tangent becomes

`y-4=2(x-6)`

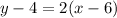
We simplify to obtain

`y=2x-12+4`

`y=2x-8`

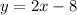
WITHOUT ELIMINATING THE PARAMETER

The given parametric equation is;

`x=6+ln(t),y=t^2+3`

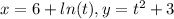
For
`x=6+ln(t)`

`(dx)/(dt)=(1)/(t)`

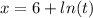
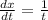
For
`y=t^2+3`

`(dy)/(dt)=2t`

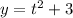
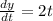
The slope is given by;

`(dy)/(dx)=((dy)/(dt) )/((dx)/(dt) )`

`(dy)/(dx)=(2t )/((1)/(t) )`

`(dy)/(dx)=2t^2`

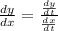
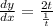
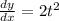
At the point, (6,4), we plug in any of the values into the parametric equation and find the corresponding value for
`t`.

Notice that

When
`x=6`,
`6=6+\ln(t)`

`6-6=\ln(t)`

`0=\ln(t)`

`e^0=e^\ln(t)`

`1=t`

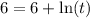
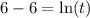
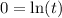
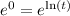
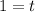
when
`y=4`,
`4=t^2+3`

`4-3=t^2`

`1=t^2`

`t=\pm1`

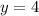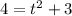
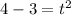
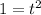
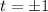
But the slope is the same when we plug in any of these values for t.

`(dy)/(dx)=2(\pm1)^2=2`

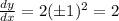
The equation of the tangent becomes

`y-4=2(x-6)`

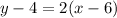
We simplify to obtain

`y=2x-12+4`

`y=2x-8`