Question

What is the cube root of
`-1000p^(12) q^(3)`?

Answer 1

Answe-10p^4q. B

Explanation:

Answer 2

You figured it out correctly, good job!

Nevertheless, let me answer the question, so that the homepage is clean and someone else might need some explanation.

We want to compute

`\sqrt[3]{-1000p^(12)q^3}`

We can break the root of a product into the product of the roots:

`\sqrt[3]{-1000p^(12)q^3} = \sqrt[3]{-1000} \cdot \sqrt[3]{p^(12)} \cdot \sqrt[3]{q^3}`

The square root of -1000 is -10, because

`(-10)^3 = -1000`

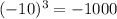
As for the exponents of the variables, taking the n-th root means to divide the exponent by n. So, in our case, we have to divide the exponents by 3:

`\sqrt[3]{p^(12)} = p^{(12)/(3)}=p^4 \quad \sqrt[3]{q^3}=q^{(3)/(3)}=q`

So, the final answer is

`\sqrt[3]{-1000p^(12)q^3} = -10p^4q`