Answer:
Function to model the amount of money;
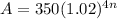
Value after 8 years;
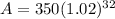
= $ 659.60
Explanation:
We apply the compound interest formula;
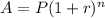
A represents the amount, P the principal invested, r is the effective rate applicable per time period and n is the time or duration.
Function to model the amount of money;
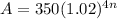
Value after 8 years;
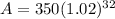
= $ 659.60