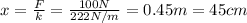Question

You exert a 100-N pull on the end of a spring. When you increase the force by 20% to 120 N, the spring's length increases 9.0 cm beyond its original stretched position. Part A: What is the spring constant of the spring? (I got k = 222 N/m)

Part B: What is its original displacement? (I can't really figure this part out)

Answer 1

A) 222 N/m

Step-by-step explanation:

Hook's law gives us the relationship between force (F), displacement with respect to the original length (x) and spring's constant (k):

`F=kx`

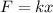
In this part of the problem, we have:

F = 120 N - 100 N = 20 N is the new force applied

x = 9.0 cm = 0.09 m is the displacement relative to the initial stretched position

Solving the equation for k, we find the spring constant

`k=(F)/(x)=(20 N)/(0.09 m)=222 N/m`

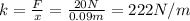
B) 45 cm

We can use Hook's law also for this part of the exercise:

`F=kx`

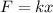
where this time we have

F = 100 N (the original pull applied)

k = 222 N/m

Solving the equation for x, we find the original displacement:

`x=(F)/(k)=(100 N)/(222 N/m)=0.45 m=45 cm`