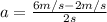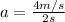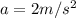The answers would be:
A. Frame of reference
E. Relative Motion
H. Speed
D. Vector
B. Distance
J. Velocity
I. Average speed
G. Displacement
C. Instantaneous Speed
F. Acceleration
Here is more about each in general:
Frame of reference is a point or location where you are doing measurements from that is not accelerating or let's say the measurement of distance and velocity of objects from your point of view.
Let's say you and a friend are sitting in a bus that is moving at 5/s. If you look at your friend, you would say that your friend is not moving or has a velocity of 0 m/s, but when you look outside, you'll see trees moving past you at the speed your bus is moving, which is 5 m/s.
Relative motion is best explained with an example
Let's say you are on a boat and your friend is standing on the pier. You are both facing the same direction and you are not both not moving. If you threw a rock in the water, you would be both seeing the same thing. The rock would move relative to both of your positions. But let's say the boat you are on starts to move and you hold onto the rock.
The rock relative to you is not moving, but the rock relative to your friend is moving the same speed as the boat.
The slope in a distance-time graph is the speed. When you look at a graph, the slope shows the change of y over the change of x. So in a distance-time graph, the distance is in the y-axis while the time is on the x axis.
Speed is defined by the change in distance over time.
Slope = (y2 - y1) Speed = distance
(x2 - x1) time
Vector is a quantity that describes both magnitude and direction. Displacement is an example of a vector quantity such as:
30m North 30m = magnitude North = direction
This differs from distance, which is a scalar quantity. It shows how far one traveled from start to end, regardless of the direction.
For example a man walks to his house from work. He walks 5m straight, takes a left and walks another 2m and walks 6m more. If you will calculate the distance he traveled, just add up the different lengths.
5m + 2m + 6m = 13m
But if you were to get the displacement, you would draw a direct line from the starting point and the end point. So in other words, displacement is the distance between the starting point and the end point, with direction.
Velocity is a vector quantity because it not only shows the distance traveled over a unit of time, it also shows direction. For example, a car is moving 5 m/s towards the East.
5 m/s = magnitude Towards the East= direction
This differs from speed because speed merely says how fast an object is moving, but it will not tell you what direction it is moving.
Average speed is computed by the formula:
v = distance/time traveling
So all you need to do is get the length traveled and divided by how long it took to travel that path. Again, average speed is a scalar, it does not say anything about the direction.
Instantaneous velocity is the change in motion at a specific point in time. For example, you have a car that is already moving and it covered a distance of 2m in 1s at one point. You want to find out the instantaneous velocity at that point. So how do you get it, just divide the distance by time:
2m/1s = 2m/s
The car was traveling at 2m/s at that moment.
Acceleration is the rate of change in velocity. It is computed with the formula:


So it is the change in velocity over the time it took for the change of velocity to occur.
For example, you have a car that was moving at a velocity of 2 m/s east and increased velocity to 6 m/s over 2 seconds.
So to solve it: