Question

A rectangular loop of wire with dimensions 1.80 cm by 9.00 cm and resistance 0.800 Ω is being pulled to the right out of a region of uniform magnetic field. The magnetic field has magnitude 2.60 T and is directed into the plane of (Figure 1) .

a) At the instant when the speed of the loop is 3.00 m/s and it is still partially in the field region, what is the magnitude of the force that the magnetic field exerts on the loop?
b) What is the direction of the force that the magnetic field exerts on the loop?

Answer 1

a) The magnitude of the magnetic force on the rectangular loop is 0.1395 N.

b) The force direction is upward, following the right-hand rule with the magnetic field pointing into the plane of the loop.

To find the force exerted by the magnetic field on the rectangular loop, you can use the formula for the magnetic force on a current-carrying wire segment in a magnetic field:

`\[ F = BIL \sin(\theta) \]`

where:

-
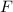`\( F \)` is the magnetic force,

-
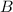`\( B \)` is the magnetic field strength,

-
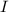`\( I \)` is the current,

-
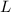`\( L \)` is the length of the wire segment in the magnetic field, and

-
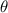`\( \theta \)` is the angle between the current direction and the magnetic field direction.

For a rectangular loop, the current flows along the length of the wire. The magnitude of the current
`(\( I \))` is given by Ohm's Law:
`\( I = (V)/(R) \)` , where
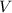`\( V \)` is the velocity of the loop and \( R \) is the resistance of the loop.

Let's calculate the force:

a) Magnitude of the Force (\( F \))

`\[ I = (V)/(R) \]`

`\[ I = (V)/(R) \]`

`\[ I = 3.75 \, \text{A} \]`

Now, use the magnetic force formula:

`\[ F = BIL \sin(\theta) \]`

For a rectangular loop,
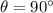`\( \theta = 90^\circ \)` because the magnetic field is directed into the plane of the loop.

`\[ F = (2.60 \, \text{T})(3.75 \, \text{A})(0.0180 \, \text{m}) \]`

`\[ F = 0.1395 \, \text{N} \]`

So, the magnitude of the force is
`\( 0.1395 \, \text{N} \).`

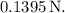
b) Direction of the Force

The direction of the force is given by the right-hand rule. Point your index finger in the direction of the magnetic field, your middle finger in the direction of the current, and your thumb will point in the direction of the force.

In this case, the force will be directed upward out of the plane of the loop.

So, the direction of the force is upward.