Assignment:
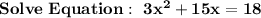
<><><><><><><>
Answer:
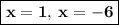
<><><><><><><>
Explanation:
<><><><><><><>
[ Step One ] Subtract 18 From Both Sides
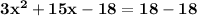
[ Step Two ] Simplify
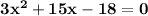
[ Step Three ] Solve With Quadratic Formula
Note:
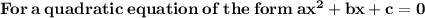
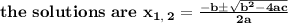
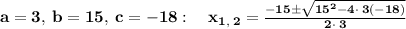
<><><><><><><>
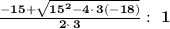
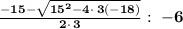
[ Step Four ] Combine Solutions
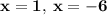
<><><><><><><>