Question

Two identical objects go around circles of identical diameter, but one object goes around the circle twice as fast as the other. The centripetal force required to keep the faster object on the circular path is 1. four times as much force as required to keep the slower object on the path. 2. half as much force as required to keep the slower object on the path. 3. one fourth as much force as required to keep the slower object on the path. 4. twice as much force as required to keep the slower object on the path. 5. the same force required to keep the slower object on the path.

Answer 1

1. four times as much force as required to keep the slower object on the path.

Step-by-step explanation:

The centripetal force that keeps the object on a circular path is given by

`F=m(v^2)/(r)`

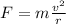
where

m is the mass of the object

v is its tangential speed

r is the radius of the circular path

In this problem, we have a second identical object (so, same mass) that moves around a circle of same diameter of the first one (so, same radius), but with a speed that is twice the speed of the first one: v' = 2v. Therefore, its centripetal force will be

`F'=m(v'^2)/(r)=m((2v)^2)/(r)=4m(v^2)/(r)=4F`

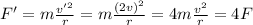
So, the centripetal force required to keep the second object on the circular path is

1. four times as much force as required to keep the slower object on the path.