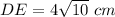Question

PLEASE HELP.

given the following diagram.

A) Name the radii ______ Name the tangents _____
B) If given that AC is 6 cm and AE is 14, what is DE? show all work.

Answer 1

Part a) The radii are segments AC and AD and the tangents are the segments CE and DE

Part b)
`DE=4√(10)\ cm`

Explanation:

Part a)

we know that

A radius is a line from any point on the circumference to the center of the circle

A tangent to a circle is a straight line which touches the circle at only one point. The tangent to a circle is perpendicular to the radius at the point of tangency.

In this problem

The radii are the segments AC and AD

The tangents are the segments CE and DE

Part b)

we know that

radius AC is perpendicular to the tangent CE

radius AD is perpendicular to the tangent DE

CE=DE

Triangle ACE is congruent with triangle ADE

Applying the Pythagoras Theorem

`AE^(2)=AC^(2)+CE^(2)`

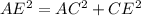
substitute the values and solve for CE

`14^(2)=6^(2)+CE^(2)`

`CE^(2)=14^(2)-6^(2)`

`CE^(2)=160`

`CE=√(160)\ cm`

`CE=4√(10)\ cm`

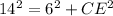
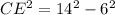
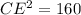
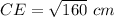
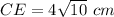
remember that

CE=DE

so

`DE=4√(10)\ cm`