Question

What is the discontinuity of the function f(x) = the quantity of x squared minus 4 x minus 12, all over x plus 2 ?

Answer 1

AlonsoDehner said the answer is C. (-2, -8)

Answer 2

x=-2 is the removable discontinuity of the function.

Explanation:

Given that

`f(x) = (x^2-4x-12)/(x+2)`

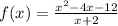
We have to find the discontinuity of the function.

We find the numerator has got a factor as denominator because

`x^2-4x-12 =(x-6)(x+2)`

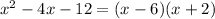
x+2 can be cancelled and the function would be

x-6 if x not equals -2

Thus the function is discontinuous at x=-2

The discontinuity is removable if f(-2) is defined as =-8

Thus x=-2 is a removable discontinuity of the function.