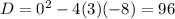Answer:
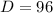
Explanation:
You must add 2 to both sides of the equation:
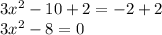
You can find the discriminant of the quadratic equation given in the problem with the formula shown below:

Based on the given equation, you have that:

Susbstitute values. Then you obtain: