Question

suppose that normal human body temperatures are normally distributed with a mean of 37°C and a standard deviation of 0.2°C what percent of humans have a temperature between 36.6°C and 37.4°C? which normal curve is shaded correctly for this problem

Answer 1

Notice that 36.6 = 37 - 2*0.2 and 37.4 = 37 + 2*0.2, so the range of temperatures 36.6 to 37.4 fall within 2 standard deviations of the mean. The empirical rule says the approximate percentage of humans with body temperatures in this range is 95%.

Answer 2

95%.

Explanation:

We have been given that the normal human body temperatures are normally distributed with a mean of 37°C and a standard deviation of 0.2°C. We are asked to find the percentage of of humans have a temperature between 36.6°C and 37.4°C.

First of all, we will find z-score corresponding to both values as:

`z=(x-\mu)/(\sigma)`

`z=(36.6^(\circ)C-37^(\circ)C)/(0.2^(\circ)C)}`

`z=(-0.4^(\circ)C)/(0.2^(\circ)C)}`

`z=-2`

`z=(x-\mu)/(\sigma)`

`z=(37.4^(\circ)C-37^(\circ)C)/(0.2^(\circ)C)}`

`z=(0.4^(\circ)C)/(0.2^(\circ)C)}`

`z=2`

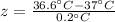
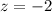
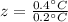
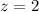
We can see that both z-scores lies within two standard deviation of the mean.

By empirical rule 68% of data points on normal distribution lies within one standard deviation of the mean.

95% of data points on normal distribution lies within two standard deviations of the mean.

99.7% of data points on normal distribution lies within three standard deviations of the mean.

Therefore, 95% of humans have a temperature between 36.6°C and 37.4°C.