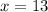Question

Solve: 2 ln 3 = ln(x - 4)​

Answer 1

2 ln 3 = ln(x-4)

ln(3^2) = ln(x-4)

3^2 = x - 4

x = 3^2 +4 = 9 +4 = 13

Answer 2

The value of x is:

`x=13`

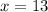
Explanation:

We are asked to solve the equation:

`2\ln 3=\ln (x-4)`

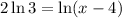
i.e. we are asked to find the value of x which satisfies the equation.

We know that:

`a\ln b=\ln b^a`

i.e.

`2\ln 3=\ln 3^2\\\\i.e.\\\\2\ln 3=\ln 9`

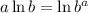
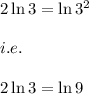
i.e. the equation is written as:

`\ln 9=\ln (x-4)`

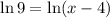
Now on taking exponential on both the side of the equation we get:

`e^(\ln 9)=e^(\ln (x-4))\\\\i.e.\\\\9=x-4`

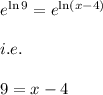
since,

`e^(\ln x)=x`

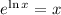
Hence, we get:

`x=9+4\\\\i.e.\\\\x=13`

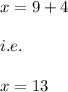
The answer is:
`x=13`