Answer: The correct option is (C) 5.
Step-by-step explanation: Given that a group of distinct objects can be arranged in 120 different ways.
We are to find the number of objects in the group.
We know that a group of n distinct objects can be arranged in n! ways.
And, for a non-negative integer n, the factorial of n is defined as

Option (A) : If n = 3, then
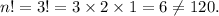
So, option (A) is incorrect.
Option (B) : If n = 4, then
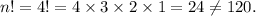
So, option (B) is incorrect.
Option (C) : If n = 5, then
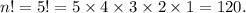
So, option (C) is correct.
Option (D) : If n = 6, then
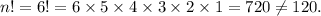
So, option (D) is incorrect.
Thus, (C) is the correct option.