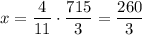4
If two triangles are similar, corresponding sides are in proportion. So, we have
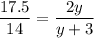
Multiply both sides by
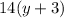 to get
to get
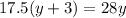
Expand the left hand side:
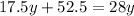
Subtract 17.5y from both sides:
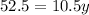
Divide both sides by 10.5:
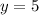
8
Given the ratio
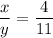
we can deduce
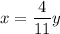
The perimeter of the rectangle is given by
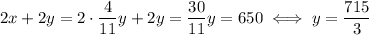
Now we can deduce the value for x: