Question

Find the lateral area the regular pyramid.

L. A. =

Answer 1

`18√(91)`

Answer 2

Answer:
`18√(91)`

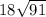
Explanation:

You must apply the following formula for calculate the lateral area the regular pyramid:

Where p is the perimeter of the base and l is the slant height:

`LA=(p*l)/(2)`

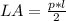
Find the apothem of the hexagonal base:

`a=(s)/(2tan((180)/(n)))`

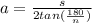
Where s is the side length and n is the number of sides the polygon.

`s=6\\n=6`

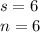
Then:

`a=(6)/(2tan((180)/(6)))`

`a=3√(3)`

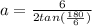
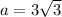
Apply the Pythagorean Theorem to find the slant height:

`l=\sqrt{(3√(3))^2+8^2}=√(91)`

The perimeter is:

`p=6*s=6*6=36`

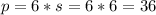
Susbtituting values, you obtain:

`LA=(36*√(91))/(2)=18√(91)`