Question

Does this sequence converge or diverge? \left\{\frac{10n-6}{2n-3}\right\} { 2n−3 10n−6 ​ }

Answer 1

The sequence converges

Explanation:

Given the sequence Un = 10n-6/2n-3

To determine whether the sequence converges or diverges, we will have to take the limit of the sequence as n goes large.

`\lim_(n \to \infty) \left\{(10n-6)/(2n-3)\right}\\`

Divide through by n

`= \lim_(n \to \infty) \left\{(10n/n-6/n)/(2n/n-3/n)\right}\\= \lim_(n \to \infty) \left\{(10-6/n)/(2-3/n)\right}\\= \left\{(10-6/\infty)/(2-3/\infty)\right}\\= (10-0)/(2-0)\\= 10/2\\= 5`

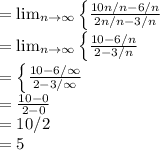
Since the limit of the sequence gives a finite value, hence the sequence converges