Question

Vectors hw, plz help

Answer 1

It's the same as the 1st one

Answer 2

This can be seen by observing that the graph is a cubic curve that passes through the origin and has a point of inflection at (0, 0). This matches the equation y =
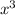`x^3`. Therefore, the answer is: B: y =
`x^3`.

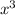The image shows a graph of a function that is increasing at an exponential rate.

The graph is concave up, which means that the second derivative of the function is positive.

The graph also passes through the point (1, 1).

The function that matches this graph is:

y =
`e^x`

This function is increasing at an exponential rate because the exponent is x.

The function is concave up because the second derivative of the function is
`e^x`, which is always positive.

The function passes through the point (1, 1) because
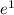`e^1` = 1.

Here is why the other functions do not match the graph:

y =
`x^2` is a parabolic function that opens upwards.

It is not increasing at an exponential rate, and it is not concave up for all values of x.

y =
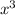`x^3` is a cubic function that passes through the origin.

It is not increasing at an exponential rate, and it is not concave up for all values of x.

y = log(x) is a logarithmic function that passes through the point (1, 0).

It is not increasing at an exponential rate, and it is concave down for all values of x.

y = 2x is a linear function.

It is not increasing at an exponential rate, and it is not concave up or down.

Therefore, the only function that matches the graph is y =
`e^x`.

Here is an example of how to use the function y =
`e^x` to solve a problem:

Problem: What is the value of y when x = 2?

Solution:

We can plug x = 2 into the function y =
`e^x` to get:

y =
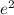`e^2` = 7.38905609893065

Therefore, the value of y when x = 2 is 7.38905609893065.