Perform the indicated operation 5/2x+3y divided by 10/4x^2-9y^2

Question

asked May 14, 2020 141k views

2 Answers

Ievche · Answer 1 · 2020-05-19T17:05:57+0000

Answer:

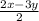
(2x-3y)/(2)

Explanation:

Dividing by a fraction means multiplying by the reciprocal. So we can write the problem as:

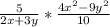
(5)/(2x+3y)*(4x^2-9y^2)/(10)

We can simplify
4x^2-9y^2 into
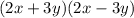(2x+3y)(2x-3y) by using the formula
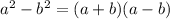
a^2-b^2=(a+b)(a-b)

Now we can write:

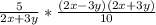
(5)/(2x+3y)*((2x-3y)(2x+3y))/(10)

We can cancel out (2x+3y) and also reduce "5" and 10". Thus we have:

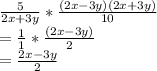
$(5)/(2x+3y)*((2x-3y)(2x+3y))/(10)\\=(1)/(1)*((2x-3y))/(2)\\=(2x-3y)/(2)$

This is the simplified form.