Answer:
the last container, the rectangular solid, has the greatest surface area.
Explanation:
Surface Area is the area of all the surfaces.
Figure 1 is a Cone. Surface Area of Cone is given by the formula
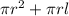
The slant height (l) is 10 and the radius is 3 (half of 6). Plugging in we get:
Surface Area =
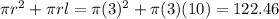
Figure 2 is a cylinder. Surface area of cylinder is given by the formula
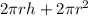
The radius is 3 and the height is 10. Pluggin in gives us:
Surface Area =
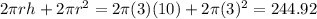
Figure 3 is a pyramid. This has 4 triangular faces each with length 6 and height 10 and one square with side 6.
Surface Area =

Plugging in the values, we get:
Surface Area =
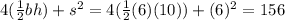
Figure 4 is a rectangular solid with length 6, width 6 and height 10. The surface area is area of all the 6 surfaces. So we have:
Surface Area =
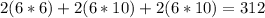
Hence, the last container, the rectangular solid, has the greatest surface area.