Question

PLEASE HELP, I'M ACTUALLY DESPERATE:(!!!!!!!!!!!!!!!!!!!!!!!!!!!

1.) Calculate the volume of the figure. Use 3.14 for π. Enter your answer as the number of m3, rounded to the nearest hundredth if necessary, like this: 42.53

2.)The volume of a sphere with a radius of 5cm is approximately _[blank]_ cm3. Enter the value that correctly fills in the blank in the previous sentence.
Use 3.14 for π, and round your answer to the nearest hundredths place if necessary.

Answer 1

1. First we start off with the volume of a cylinder

`v = (3.14 * {r}^(2) )h`

Since we have all of the numbers for the formula, we plug them into it...

`v = (3.14 * {4}^(2) ) * 9`

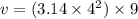
We calculate this in a calculator and get 452.16 m3. However, this equation is not finished, we still have to calculate the volume of the half sphere.

The formula for the volume of a regular sphere is

`v = (4)/(3) (3.14 * {r}^(3) )`

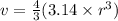
All we have to do is divide it in half after we find the area of the whole sphere.

`(4)/(3) (3.14 * {4}^(3))`

We calculate this to get 267.95 m3.

We add both of the cylinder and the half spheres volumes together and get 720.11 m3.

2. For this problem, we need to go back and get our formula for a sphere...

`v = (4)/(3) (3.14 * {r}^(3) )`

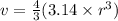
Since we already know the radius, all we need to do is plug it into the formula...

`v = (4)/(3) (3.14 * {5}^(3) )`

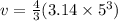
When we calculate all of it we end up with 523.33 cm3.