Answer:
0, 5 and 9
Explanation:
The critical points for any inequality are the points for which the numerator of the denominator equal 0.
Here, we are given the following inequality:
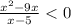
So the critical points will be where
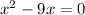 and where
and where
 .
.
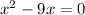
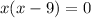
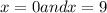

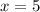
Therefore, the critical points for the given inequality are 0, 5 and 9.