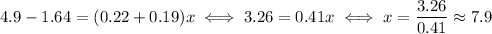a. We know the rates of change for both companies, as well as the starting values in 2013. So, to predict the values in 2022 we have to simulate the passing of 9 years. Company A loses 0.22 billions per years, so they will lose
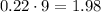 billions in 9 years. So, we have
billions in 9 years. So, we have

Similarly, company B will have
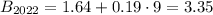
billion dollars in 2022.
b. This question is similar to the previous one, except this time we have to find the number of years necessary to reach a particular goal. We have
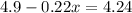
Solving for x, we have

c. We know the behaviour of the two values, so the number of years will again be the unkown, and we set the two values to be the same:

Solving for x, we have