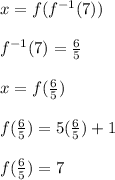Answer:
A.
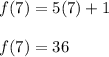
B.
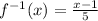
C.
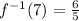
D.
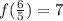
Explanation:
A. To solve the first part of the problem we must replace
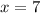 in the function
in the function
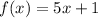
So:
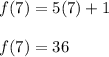
B. In part B we must find the inverse function of
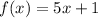
To find the inverse function do
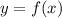
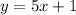
Now clear the variable x.

Replace x with y.
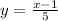
Finally
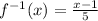
C. Now we take the inverse function found above and replace
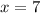
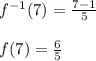
D. Now we substitute
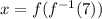 in the original function.
in the original function.