Answer:
(–0.708, 0.50) and (0.708, 0.50)
Explanation:
We are given the following two equation and have to determine the approximate points at which these equation are equal:
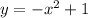 and
and

I have graphed these two equations as you can see below.
Here, points of intersection will be the solutions to a system of equation.
From the graph, I can say the point is about (–0.708, 0.50) and the other point where the two equations meet is nearly (0.708, 0.50).
So my approximate points are (–0.708, 0.50) and (0.708, 0.50).