Answer:
Option D)
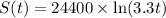
The average rate of change in Elija's salary between is $7452.50 per year.
Explanation:
We are given the following in the question:
S(t) represent the Elija's salary.
S(t) can be obtained by multiplying starting annual salary, $24,400, by the natural logarithm of the product of 3.3 and the number of years since 2010, t.
Thus, we can write:
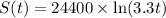
Average rate of change of function =
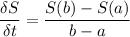
Putting b = 2015-2010 = 5, a = 2012-2010 = 2
We evaluate S(5) and S(2)
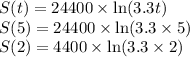
Average rate of change =
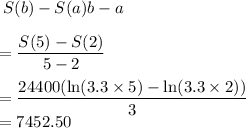
The average rate of change in Elija's salary is $7452.50 per year.