For this case, we have a function of the form:
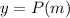
Where "y" represents the number of problems completed.
We must find the inverse function of:
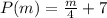
For this, we perform the following steps:
We change P(m) to y:
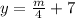
We clear the variable "m":

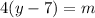
We change m to
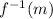 :
:

Taking into account that "y" represents the number of problems completed, we substitute "y" for "p":
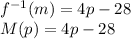
Answer:
Option D