Question

Graph the line using a point and a slope. Write the equation of each line.

C) a line that contains point (0, −3) and perpendicular to another line whose slope is 2.

Answer 1

`y=-(x)/(2)-3`

Explanation:

If two lines having slopes
`m_1` and
`m_2` are perpendicular,

`m_1* m_2=-1`

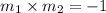
Thus, if the slope of the line perpendicular line with slope 2 is m,

Then,

`m* 2=-1\implies m = -(1)/(2)`

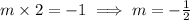
Now, the equation of the line passes through
`(x_1, y_1)` with slope m is,

`y-y_1=m(x-x_1)`

Hence, the equation of the line contain (0, -3) with slope
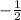`-(1)/(2)` is,

`y+3=-(1)/(2)(x-0)`

`y=-(1)/(2)x-3`

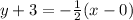
Graphing :

if x = 0, y = -3,

if y = 0,
`-(x)/(2)=3` ⇒ x = -6

Thus, by joining the points (0, -3) and (-6, 0) we will get the graph of the given line.

Answer 2

y = -1/2x -3

Explanation:

The line perpendicular to one with a slope of 2 will have a slope that is the negative reciprocal of 2, that is, -1/2. The given point is the y-intercept of the required line, so we can write its equation directly in slope-intercept form:

y = mx + b

where m is the slope (-1/2), and b is the y-intercept (-3). Your line is ...

y = -1/2x -3