Hello!
The answer is: The length of the rectangle is 28 inches, while the width is 23 inches.
Why?
Perimeter is equal to the sum of all of the sides of the rectangle:

We know that the perimeter is 102 inches and width is 9 inch more than half of the length, so:
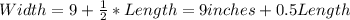
So, substituting the Width into the first equation, we have:
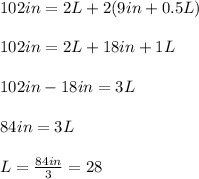
Then, substituting L into the second equation, we have:
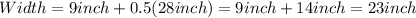
So, the length of the rectangle is 28 inches, while the width is 23 inches.
Have a nice day!