Answer:
a) The initial speed of the projectile is approximately 42.410 meters per second.
b) The speed of the projectile after 4 seconds is approximately 21.352 meters per second.
c) The horizontal range of the projectile is 169.64 meters.
d) The maximum height of the projectile is 68.775 meters.
e) The speed of the projectile when it landed on the ground is approximately 46.807 meters per second.
Step-by-step explanation:
According to the statement, the projects shows a parabolic motion, which consists in the combination of horizontal uniform motion and vertical uniformly accelerated motion due to gravity. This motion is represented by the following equations of motion:
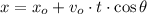 (1)
(1)
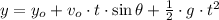 (2)
(2)
Where:
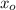 ,
,
 - Initial and current horizontal position, measured in meters.
- Initial and current horizontal position, measured in meters.
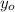 ,
,
 - Initial and current vertical position, measured in meters.
- Initial and current vertical position, measured in meters.
 - Launch angle, measured in sexagesimal angle.
- Launch angle, measured in sexagesimal angle.
 - Gravitational acceleration, measured in meters per square second.
- Gravitational acceleration, measured in meters per square second.
 - Time, measured in second.
- Time, measured in second.
a) By using (2) and knowing that
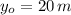 ,
,
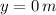 ,
,
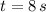 ,
,
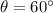 and
and
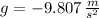 , then initial speed of the projectile is:
, then initial speed of the projectile is:
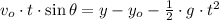
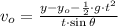

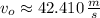
The initial speed of the projectile is approximately 42.410 meters per second.
b) The vertical component of the velocity of the projectile is determine by differentiating (2) in time and substitute all known values:
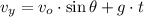 (3)
(3)
(
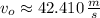 ,
,
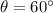 ,
,
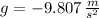 and
and
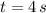 )
)
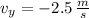
The horizontal component of the velocity of the projectile is:

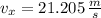
And the speed of the projectile is determined by Pythagorean Theorem:
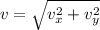
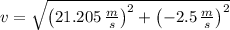

The speed of the projectile after 4 seconds is approximately 21.352 meters per second.
c) By (1) we find the horizontal range of the projectile:
(
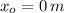 ,
,
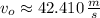 ,
,
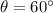 ,
,
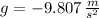 and
and
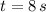 )
)
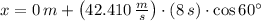

The horizontal range of the projectile is 169.64 meters.
d) The projectile reaches its maximum height when velocity is zero. By (3) and knowing that
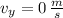 ,
,
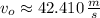 and
and
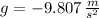 , the time associated with maximum height is:
, the time associated with maximum height is:
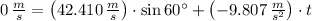
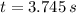
And by (2) and knowing that
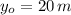 ,
,
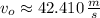 ,
,
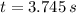 ,
,
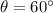 and
and
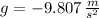 , the maximum height reached by the projectile is:
, the maximum height reached by the projectile is:

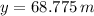
The maximum height of the projectile is 68.775 meters.
e) If we know that
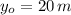 ,
,
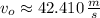 ,
,
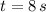 ,
,
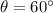 and
and
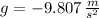 , the components of the speed are, respectively:
, the components of the speed are, respectively:
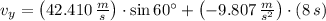
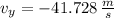

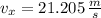
And the speed of the projectile is determined by Pythagorean Theorem:
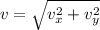
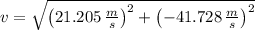

The speed of the projectile when it landed on the ground is approximately 46.807 meters per second.