Answer:
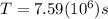
According to the Third Kepler’s Law of Planetary motion “The square of the orbital period of a planet is proportional to the cube of the semi-major axis (size) of its orbit”.
In other words, this law states a relation between the orbital period
 of a body (planet Mercury in this case) orbiting a greater body in space (the Sun) with the size
of a body (planet Mercury in this case) orbiting a greater body in space (the Sun) with the size
 of its orbit.
of its orbit.
This Law is originally expressed as follows:
 (1)
(1)
Where;
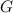 is the Gravitational Constant and its value is
is the Gravitational Constant and its value is
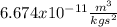
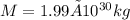 is the mass of the Sun
is the mass of the Sun
![r=5.79×10^(10)m is the <strong>distance from Mercury to the Sun</strong> (assuming it is a circular orbit, the semimajor axis is equal to the radius of the orbit). </p><p> </p><p>If we want to find the period, we have to express equation<strong> (1)</strong> as written below and substitute all the values: </p><p> </p><p>[tex]T=\sqrt{(4\pi^(2))/(GM)r^(3)}](https://img.qammunity.org/2020/formulas/physics/high-school/3ftdo5wx7un1jd3ae2f2hopzrabv7onz0y.png) (2)
(2)
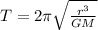 (3)
(3)
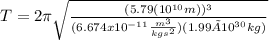 (4)
(4)
Solving and taking into account that
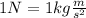 :
:
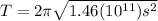 (5)
(5)
Finally:
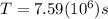 >>>>This is the period of revolution for the planet Mercury
>>>>This is the period of revolution for the planet Mercury