Question

What must be the molarity of an aqueous solution of trimethylamine, (ch3)3n, if it has a ph = 11.20? (ch3)3n+h2o⇌(ch3)3nh++oh−kb=6.3×10−5?

Answer 1

0.040 mol / dm³. (2 sig. fig.)

Step-by-step explanation

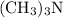`(\text{CH}_3)_3\text{N}` in this question acts as a weak base. As seen in the equation in the question,
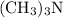`(\text{CH}_3)_3\text{N}` produces
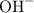`\text{OH}^(-)` rather than
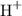`\text{H}^(+)` when it dissolves in water. The concentration of
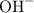`\text{OH}^(-)` will likely be more useful than that of
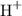`\text{H}^(+)` for the calculations here.

Finding the value of
`[\text{OH}^(-)]` from pH:

Assume that
`\text{pK}_w = 14`,

`\begin{array}{ll}\text{pOH} = \text{pK}_w - \text{pH} \\ \phantom{\text{pOH}} = 14 - 11.20 &\text{True only under room temperature where }\text{pK}_w = 14 \\\phantom{\text{pOH}}= 2.80\end{array}`.

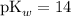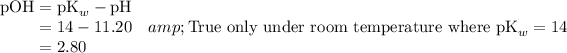`[\text{OH}^(-)] =10^{-\text{pOH}} =10^(-2.80) = 1.59\;\text{mol}\cdot\text{dm}^(-3)`.

Solve for
`[(\text{CH}_3)_3\text{N}]_\text{initial}`:

`\frac{[\text{OH}^(-)]_\text{equilibrium}\cdot[(\text{CH}_3)_3\text{NH}^(+)]_\text{equilibrium}}{[(\text{CH}_3)_3\text{N}]_\text{equilibrium}} = \text{K}_b = 1.58* 10^(-3)`

Note that water isn't part of this expression.

The value of Kb is quite small. The change in
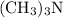`(\text{CH}_3)_3\text{N}` is nearly negligible once it dissolves. In other words,

`[(\text{CH}_3)_3\text{N}]_\text{initial} = [(\text{CH}_3)_3\text{N}]_\text{final}`.

Also, for each mole of
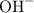`\text{OH}^(-)` produced, one mole of
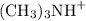`(\text{CH}_3)_3\text{NH}^(+)` was also produced. The solution started with a small amount of either species. As a result,

`[(\text{CH}_3)_3\text{NH}^(+)] = [\text{OH}^(-)] = 10^(-2.80) = 1.58* 10^(-3)\;\text{mol}\cdot\text{dm}^(-3)`.

`\frac{[\text{OH}^(-)]_\text{equilibrium}\cdot[(\text{CH}_3)_3\text{NH}^(+)]_\text{equilibrium}}{[(\text{CH}_3)_3\text{N}]_\textbf{initial}} = \text{K}_b = 1.58* 10^(-3)`,

`[(\text{CH}_3)_3\text{N}]_\textbf{initial} =\frac{[\text{OH}^(-)]_\text{equilibrium}\cdot[(\text{CH}_3)_3\text{NH}^(+)]_\text{equilibrium}}{\text{K}_b}`,

`[(\text{CH}_3)_3\text{N}]_\text{initial} =((1.58*10^(-3))^(2))/(6.3*10^(-5)) = 0.040\;\text{mol}\cdot\text{dm}^(-3)`.