Question

Prove that SinA+Sin(120+A)+Sin(240+A)=0

Answer 1

see explanation

Explanation:

Using the Addition formula for sine

• sin(x + y) = sinxcosy + cosxsiny

and sin120° = sin60°, cos120° = - cos60°

sin240° = - sin60°, cos240°, cos240° = - cos60°

-------------------------------------------------------------------

Consider the left side

Second term

sin(120 + A) = sin120cosA + cos120sinA

= sin60cosA - cos60sinA

Third term

sin(240 + A)

= sin240cosA + cosAsin240

= - sin60cosA - cos60sinA

--------------------------------------------------------------------

Putting the 3 terms together

sinA + sin60cosA - cos60sinA - sin60cosA - cos60sinA

= sinA - 2cos60sinA

= sinA - (2 ×
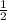`(1)/(2)`)sinA

= sinA - sinA

= 0 = right side ⇒ proven