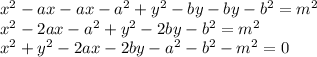Question

What is the general form of the equation of a circle with center at (a,b) and radius of length m​

Answer 1

`x^2 + y^2 -2ax -2by -a^2-b^2 -m^2 = 0`

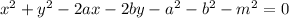
Explanation:

The vertex form of an equation is
`(x-h)^2 + (y-k)^2 = r^2` and it has a center (h,k) and radius r which forms it. To write the general form, start with the vertex form and expand it out.

Here the center is (a,b) so h=a and k=b. Substitute these values with the radius r = m.

`(x-a)^2 + (y-b)^2 = m^2`

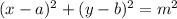
Expand out the exponents.

`x^2 -ax -ax -a^2 + y^2 - by - by - b^2 = m^2\\x^2 -2ax -a^2 + y^2 -2by -b^2 = m^2\\x^2 + y^2 -2ax -2by -a^2-b^2 -m^2 = 0`