Answer:
1.
t = 0.9 sec
2.
Option a is correct. t = 3 sec
3.
Option C is correct, h(3) = 344 feet
Explanation:
1.
The equation that determine the Ryan baseball is given by:
 ....[1]
....[1]
where,
h(t) is the height after t time
a is the acceleration i.e, a ≈ 10 m/s^2
 is the initial velocity
is the initial velocity
 is the initial height from the ground.
is the initial height from the ground.
As per the statement:
Ryan throws a baseball upward with an initial velocity of 12 m/s from a height of 2m above the ground.
⇒
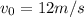 and
and
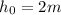
Substitute the given values we have;

We have to find how long will it take for the baseball to hit the ground.
⇒ h(t) = 0
then;
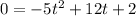
Simplify:
t = 2.556 and t = -0.156
Since, t cannot be negative.
Therefore, 2.6 sec long will it take for the baseball to hit the ground.
2.
Given that:
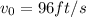 and
and
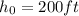 and use a ≈ 32ft/s^2
and use a ≈ 32ft/s^2
then;
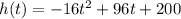
To find the maximum height:
A quadratic equation
 then the axis of symmetry is given by:"
then the axis of symmetry is given by:"
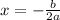
For
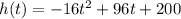 we have;
we have;
Using axis of symmetry;
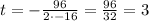 sec
sec
Therefore, 3 sec does it take for the ball to reach its maximum height.
3.
Similar ques as ques no 2.
We have to find maximum height that the ball will reach
Substitute t =3 sec in
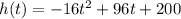 to find h(3) we have;
to find h(3) we have;
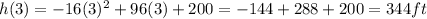
Therefore, the the maximum height that the ball will reach is, 344 feet