Question

What is the value of b?

Answer 1

b = 17

Explanation:

We are given a triangle ABC with one known angle and two known side lengths and we are to find the length of the third side.

For that, we can use the cosine rule and its formula is given by:

`c = \sqrt { a^2 + b^2 - 2 ab cosC }`

Substituting the given values in the above formula:

`b = \sqrt { (28) ^ 2 + (25) ^ 2 - 2 (28) (25) cos (36.9) }`

`b=√((784)+(625)-1400*0.799)`

`b=√(289.4)`

b = 17.01

Answer 2

b = 17 (rounded to the nearest whole number)

Explanation:

When there is 1 angle given and two sides of a triangle, we can use the cosine rule to solve for the unknown side.

Cosine Rule is given by
`c^2=a^2+b^2-2abCosC`

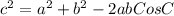
Where c is the unknown side length,

a, b are the two given sides, and

C is the angle in between the two given sides.

Plugging in all the info into the formula and solving for c, gives us:

`b^2=(28)^2+(25)^2-2(28)(25)Cos(36.9)\\\\b^2=289.4415\\b=√(289.4415)\\ b=17.01`

Rounding to nearest whole number, b = 17