Answer:
60 days
Step-by-step explanation:
Half-life is the amount of time it takes half of a substance to decay away.
Guess and Check
One method for solving half-life problems like this is to guess and check. To do this, we can continue to divide 475mg by 2 until we get to 30mg.
- 475 ÷ 2 = 237.5
- 237.5 ÷ 2 = 118.75
- 118.75 ÷ 2 = 59.375
- 59.375 ÷ 2 = 29.6875
As seen here, it takes approximately 4 half-lives for this sample of Ra-225 to decay to 30mg. Now, we can multiply 4 by the length of the half-life, 15 days.
Fractions
Another way to solve this is to use fractions.
- 16 is equivalent to
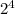 .
.
This means that it takes 4 half-lives for 475mg to decay to 30mg. Using the same method above, we can tell that 4 half-lives are 60 days.
Important Note
In this question, I rounded occasionally. So, not all of the values are exact, but they are all very close.