Answer:
The pair of equivalent expressions are 2 and 8, 3 and 7, 4 and 5.
Explanation:
Expand or factor each of the following expressions
1.

![[\because (a-b)^2=a^2-2ab+b^2]](https://img.qammunity.org/2020/formulas/mathematics/high-school/14xchlcvyv1c3qsy5ueoz3rt7wdko6uaxq.png)
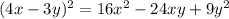
2.

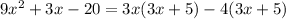
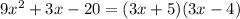
It is same as expression 8. Therefore expression 2 and 8 are equivalent.
3.
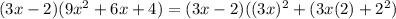

![[\because a^3-b^3=(a-b)(a^2+ab+b^2)]](https://img.qammunity.org/2020/formulas/mathematics/high-school/4r8jndxviguld1wwtv0om10i0jaffcmuhe.png)
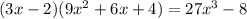
It is same as expression 7. Therefore expression 3 and 7 are equivalent.
4.
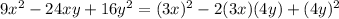
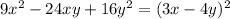
![[\because (a-b)^2=a^2-2ab+b^2]](https://img.qammunity.org/2020/formulas/mathematics/high-school/14xchlcvyv1c3qsy5ueoz3rt7wdko6uaxq.png)
It is same as expression 5. Therefore expression 4 and 5 are equivalent.
5.

6.
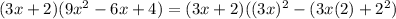

![[\because a^3+b^3=(a+b)(a^2-ab+b^2)]](https://img.qammunity.org/2020/formulas/mathematics/high-school/dmth0bkhd7x4bso4okrzsydw6x9k3qbo13.png)
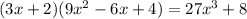
7.
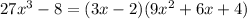
8.
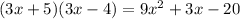
Therefore the pair of equivalent expressions are 2 and 8, 3 and 7, 4 and 5.