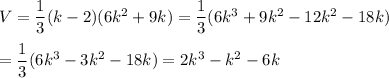Question

100 points!! Write and simplify a polynomial expression for the volume of each figure.

DISCLAIMER: IF THE ANSWERS ARE WRONG IT WILL BE REPORTED

Answer 1

`\large\boxed{1.\ V=3b^4-15b^3+3b^2-15b}\\\boxed{2.\ V=4\pi n^3-16\pi n^2+16\pi n}\\\boxed{3.\ V=2k^3-k^2-6k}`

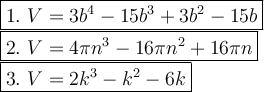
Explanation:

The picture #1:

It's a rectangular prism. The formula of a volume of a rectangular prism:

`V=lwh`

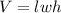
l - length

w - width

h - height

We have

`l=b+1,\ w=3b,\ h=b-5`

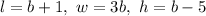
Substitute:

`V=(b+1)(3b)(b-5)`

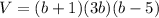
Use the distributive property a(b + c) = ab + ac

and the FOIL: (a + b)(c + d) = ac + ad + bc + bd

`V=(3b^3+3b)(b-5)=3b^4-15b^3+3b^2-15b`

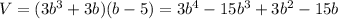
The picture #2:

It's a cone. The fomula of a volume of a cone:

`V=(1)/(3)\pi r^2h`

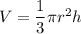
r - radius

h - height

We have:

`r=n-2,\ h=12n`

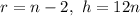
Substitute:

`V=(1)/(3)\pi(n-2)^2(12n)`

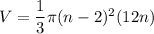
Use (a + b)² = a² + 2ab + b²

`V=(1)/(3)\pi(n^2-4n+4)(12n)=(4\pi n)(n^2-4n+4)`

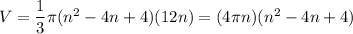
Use the distributive property:

`V=4\pi n^3-16\pi n^2+16\pi n`

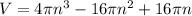
The picture #3:

It's a pyramid with a rectangle in the base. The formula of a volume of a rectangular pyramid:

`V=(1)/(3)abh`

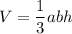
a, b - edge of a base

h - height

We have

`a=k-2, b=2k+3, h=3k`

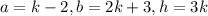
Substitute:

`V=(1)/(3)(k-2)(2k+3)(3k)`

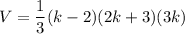
Use the distributive property and the FOIL.

`V=(1)/(3)(k-2)(6k^2+9k)=(1)/(3)(6k^3+9k^2-12k^2-18k)\\\\=(1)/(3)(6k^3-3k^2-18k)=2k^3-k^2-6k`

Answer 2

See below

Explanation:

1: (b+1)*(3b)*(b-5)

(3b^2+3b)(b-5)

3b^3-15b^2+3b^2-10b

3b^3-12b^2-10b

2: πr^ 2(h/3)

π(n-2)^2(12n/3)

π(n-2)(n-2)(12n/3)

π(n^2-2n-2n+4)(12n/3)

π(n^2-4n+4)(12n/3)

π(n^2-4n+4)(4n)

π(4n^3-16n^2+16n)

(I'm not 100% sure with this one)

3: (lwh)/3

((k-2)(2k+3)(3k))/3

((2k^2-4k+3k-6)(3k))/3

(6k^3-12k^2+9k^2-18k)/3

(6k^3-3k^2-18k)/3

2k^3-k^2-6k