Question

Determine n between 0 and 19 such that (2311)(3912) ≡ n mod 20.

Answer 1

You can write 2311 and 3912 in the form
`20q+r`:

`2311=115\cdot20+11`

`3912=125\cdot20+12`

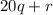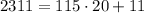
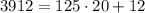
Then

`2311\cdot3912=(115\cdot20+11)(125\cdot20+12)`

`2311\cdot3912=115\cdot125\cdot20^2+(11\cdot125+12\cdot115)\cdot20+11\cdot12`

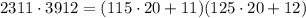
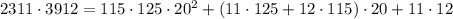
Taken modulo 20, the terms containing powers of 20 vanish and you're left with

`2311\cdot3912\equiv11\cdot12\equiv132\pmod{20}`

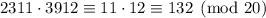
We further have

`132=6\cdot20+12`

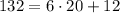
so we end up with

`2311\cdot3912\equiv12\pmod{20}`

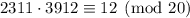
and so
`n=12`.

###

If instead you're trying to find
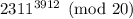`2311^(3912)\pmod{20}`, you can apply Euler's theorem. We can show that
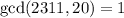`\mathrm{gcd}(2311,20)=1` using the Euclidean algorithm. Then since
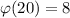`\varphi(20)=8`, and 8 divides 3912, we have

`2311^(3912)\equiv2311^(489\cdot8)\equiv(2311^(489))^8\equiv1\pmod{20}`

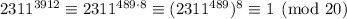
To show 2311 and 20 are coprime:

2311 = 115*20 + 11

20 = 1*11 + 9

11 = 1*9 + 2

9 = 4*2 + 1 => gcd(2311, 20) = 1