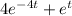Question

Inverse laplace of L^-1 {5s/s^2 + 3s - 4}​

Answer 1

`L^(-1) ((5s)/(s^(2)+ 3 s -4 ) )` =
`4e^(-4t) + e^(t)`

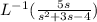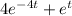
Explanation:

Step(i):-

Given

`L^(-1) ((5s)/(s^(2)+ 3 s -4 ) )`

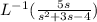
Factors of s² + 3s - 4

= s² + 4s - s -4

= s( s +4 ) -1 (s +4)

= (s-1)(s+4)

`L^(-1) ((5s)/(s^(2)+ 3 s -4 ) )`

=
`L^(-1) ((5s)/(s+4)(s-1) ) )`

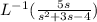
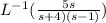
By using partial fractions

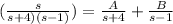`((s)/(s+4)(s-1) ) ) = (A)/(s+4) + (B)/(s-1)` ..(i)

s = A ( s-1) + B( s+4) ....(ii)

Put s= 1 in equation (ii) , we get

1 = B(5)

`B = (1)/(5)`

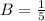
s = -4 in equation (ii) , we get

-4 = -5A

`A =(4)/(5)`

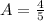
Step(ii):-

now the equation (i) , we get

`((s)/(s+4)(s-1) ) ) = (4)/(5(s+4)) + (1)/(5(s-1))`

`L^(-1) ((s)/(s+4)(s-1) ) ) = 5( L^(-1) (4)/(5(s+4)) + 5L^(-1) (1)/(5(s-1))`

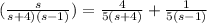
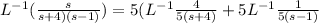
By using inverse Laplace transform formula

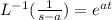
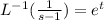
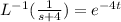
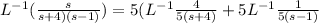
`L^(-1) ((1)/(s-a) ) = e^(at)`

`L^(-1) ((1)/(s-1) ) = e^(t)`

`L^(-1) ((1)/(s+4) ) = e^(-4t)`

`L^(-1) ((s)/(s+4)(s-1) ) ) = 5( L^(-1) (4)/(5(s+4)) + 5L^(-1) (1)/(5(s-1))`

=
`4e^(-4t) + e^(t)`